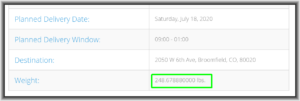
Today I went to a tracking page for Ikea’s delivery company and saw that the shipment weight was said to be “248.678880000 lbs.” This is, of course, impossible. The alert reader will perhaps already know where I am going with this. Why is this impossible? It is impossible because no commercially available scale is able to weigh things to a precision of eight significant digits. Expressed in colloquial terms, there is no scale that you or I could ever conveniently be in the same room with that would be able to distinguish between something that weighs 248.67888 pounds or 248.67889 pounds or 248.67887 pounds.
The chemistry laboratory triple-beam balance that we all used in our analytical chemistry class in college had a precision of, at best, maybe one part in one million, or at most six significant digits. So it is completely illusory for this delivery company to give the impression that it knows the weight of the Ikea shipment to eight significant digits.
Indeed the presence of the four trailing zeroes on the number might be interpreted as a representation to the reader that the value is actually known to twelve significant digits, which is laughably past being merely illusory.
It’s one thing to get this kind of thing wrong if you are a web site designer but it’s quite another if you are a patent practitioner. From time to time I run into issued patents where similar missteps have been made. See for example US patent number 6325012 which talks about an undersea habitation bubble 19 connected via a passage 20 to a mainland outside location 22. (Yes, the surface of the water is shown in this figure as sloping, which would never happen in real life.) At column 4 the practitioner says:
The air going out through the air-discharge tube is pushed out by means of the condensation unit fan by using the pressure difference between the bubble (202.650 kPa) and outside pressure (101.325 kPa) and using this parameter and the required flow, the return tube (air-discharge to main land) diameter has been calculated by using Muller’s formula.
Here the practitioner refers to the pressure at each of the two locations using six significant digits. The practitioner showed a bit of cluelessness given that most commercial gas or liquid pressure measurement sensors have a precision of no better than about 0.1% or at most about four significant digits. So it is illusory for the practitioner to suggest that the pressure in the bubble might be known to six significant digits and that the pressure outside might likewise be known to that precision. (Imagine the poor impression that this might make for a better-informed patent examiner!)
In the case of this US patent, it is very easy to work out the source of the blunder. The source document from the inventor surely referred to the air pressure at sea level as “1 atmosphere” and then somewhat arbitrarily assumed that the bubble might be at a depth of around two atmospheres. (Such a depth is around twenty meters or around sixty feet.) What probably happened next is that the patent practitioner decided that “one atmosphere” and “two atmospheres” somehow did not sound fancy enough or scientific enough. Or maybe the patent practitioner had heard in some CLE presentation that it is a good idea to use metric units when you are writing a patent application. Or maybe the patent practitioner realized that to justify the bill that was going to get sent to the client, the patent application as filed desperately needed to look different from the original disclosure document from the inventor. Anyway, for one or more of these reasons, the patent practitioner then looked up somewhere to find out the ten-dollar-word way to say “one atmosphere”, and read that this is 101.325 kiloPascals. In which case two atmospheres would be 202.650 kiloPascals. And that is what got stuffed into the patent application.
The original numbers from the inventor were at best a single significant digit, if that. But the patent practitioner gave a completely false impression that the pressures were being measured to six significant digits.
How do you feel about significant digits? What do you recall from your first-year physics class about the difference between accuracy and precision? What fond memories of your analytical chemistry class remain with you today, that you might like to share? Please post a comment below.

I never understood significant figures with respect to multiplying and dividing compared to adding or subtracting in my chemistry and physics in college… so I think I did something like rounded up to the decimal place with to the number of significant digits the number with the most decimal places has and then sometimes added or subtracted one decimal position depending on what I felt in my gut was the most accurate. I think I got it right about 75-80% of the time. LOL. I was clueless. However, your post inspired me to finally learn and there seems to be some videos that make it significantly easier to understand than how my undergrad profs tried to explain/teach. Multiplying/Dividing https://youtu.be/Ot3XK0JZGEk, Adding/Subtracting https://youtu.be/4c-lRjCFOqo
When I worked as a European Patent Attorney for a US company, I was forever amending measurements commonly used by technical staff (like psi, thous of an inch, lbs etc.) into SI units as required by the EPO.
This often required ensuring that the numbers that I was quoting in the patent application had the appropriate precision and was always a real pain, when thicknesses and pressures were being quoted as X thous and Y psi. For example, 1 thou or 1 psi can just look ridiculous in m/mm and kPA (25.4 μm / 0.025 mm & 6.89 kPa). How does “significant figures” work here? I must admit that I often used to limit myself to 2 decimal places as this was just easier.
Well the bright-line rule is that when converting from one set of units into another set of units, preserve the same number of significant digits. Round upwards or downwards as needed to the closest value available given the limited number of significant digits.
1.01 psi would be 6.96 kPa. 1.00 psi would be 6.89 kPa. 1.0 psi would be 6.9 kPa. 1 psi would be 7 kPa.
What’s awkward of course is that what is underlying any decimal notation is communication of values that are fundamentally logarithmic. The percentage change from 2 to 3 is 50% while the percentage change from 8 to 9 is a mere 12½%. So when we say our pressure is 2 psi with one significant digit, part of what is being communicated is that the true value might be 1 psi (50% less) or 3 psi (50% more). The 2 psi pops out of the calculator as 13.7895 kPa which we are obligated to truncate to 10 kPa. The reader might think this means that we are saying the value is known to be somewhere in the range of 9 kPa to 11 kPa (10% less or 10% more).
This all forces us to admit that “significant digits” is not at all sufficient to communicate how close we think our reported value is to the true underlying value. There is really no choice but to provide more information. So we might say “2 psi plus or minus 0.2 psi”. Then we can say it is 10 psi plus or minus 1 psi. When we do it in this way with the “plus or minus” then we are no longer relying on the rather imprecise “number of significant digits” way of communicating to the reader how precisely we know our value. There are other well known and accepted ways besides “plus or minus” to communication precision. Percentages for example.
At which point we also need to acknowledge that when we try to communicate things with words and numbers, there is always a context to any particular communication. Sometimes it is really important to communicate precision like this, whether with numbers of significant digits or with “plus or minus”. But sometimes we are merely hoping to signal to the reader an order of magnitude for some value. In such a case it may not be terribly important to provide things like “plus or minus” values.
“about”
Carl,
I agree with the points you made. The following is merely for amusement (“amusement” is not really the right word, but my verbal precision is suffering from round off error at the moment)
Even if we had access to (purportedly) infinitely precise instruments, there could still be a fundamental issue with regards to the nature of reality:
https://www.quantamagazine.org/does-time-really-flow-new-clues-come-from-a-century-old-approach-to-math-20200407/